Some personal thoughts after reading WGAN paper.
Originally published at Dian Organization Blog
刚刚开始参与一些 GAN 研究,看了一下 WGAN 的论文和相关的一些博客,在这里记录一下。
首先贴 reference:
- Wasserstein GAN (the original paper)
- GAN — Wasserstein GAN & WGAN-GP
- 令人拍案叫绝的Wesserstein GAN
Wasserstein GAN(以下简称 WGAN)主要是解决了一个问题——损失函数不连续。实际上在 CS294 Deep-RL 的 Q-Learn 相关章节中也有提到过类似的问题:试想我们在训练一个 agent 玩 PONG,一开始这个 agent 由于没有被训练,只能做出随机(naive)的动作,很大概率它八辈子摸不到球。偶尔有一次我们的 agent 终于打到球了,这个时候我们的原始的 summed reward 是长这样的👇
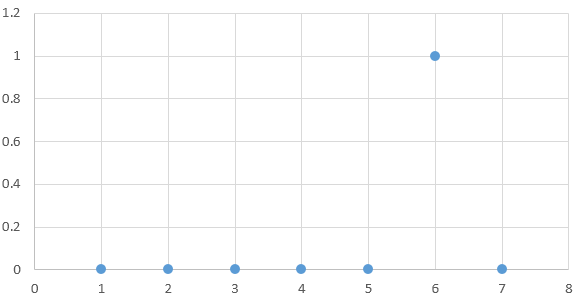
agent 在第 6 次实验中打到了球,我们给了他一个 reward 值。但你能说之前所有的动作、所有实验都对这次击球没有贡献吗?可能第 6 次与第 5 次的差别仅仅在最后一毫秒,我们的 agent 把弹板向正确的方向移动了,打了一个擦边球。擦边与不擦边,在我们的世界(analog)看来,是差不多的;但在计算机(discrete)看来,这可是完全零与非零的区别,是一个无限大倍数的提升。计算机就会认为只有第 6 次的实验是成功的,其他的都是完全失败的。这也就导致了目前 DQN(reward 不连续)、GAN(loss 不连续) 模型训练极为困难的情况,因为所有“差一点成功”的实验结果都被扔掉了,而这些实验结果在人看来,虽然不够好,但是仍然有足够的参考意义,完全有资格作为训练样本。
这也正是为什么 WGAN 使用了 Wasserstein 距离(EM 距离)作为其衡量 loss / difference 的算子。传统 GAN 在衡量两个 agent 之间相似度(本质为两个概率分布的相似度)的时候使用的是一些经典老牌的公式:KL散度,JS散度,甚至还有人用单位阶跃 \(\delta\)。。。这些公式的解空间总是存在那么些个微分性质”不好”的地方,导致算法实际跑起来的时候梯度不是爆炸就是消失。但 Wasserstein 距离是连续的,给平滑的 SGD 过程提供了非常好的微分性质基础。下图展示了 Wasserstein 优越的连续性与微分性 [from the “Wasserstein GAN” paper]。
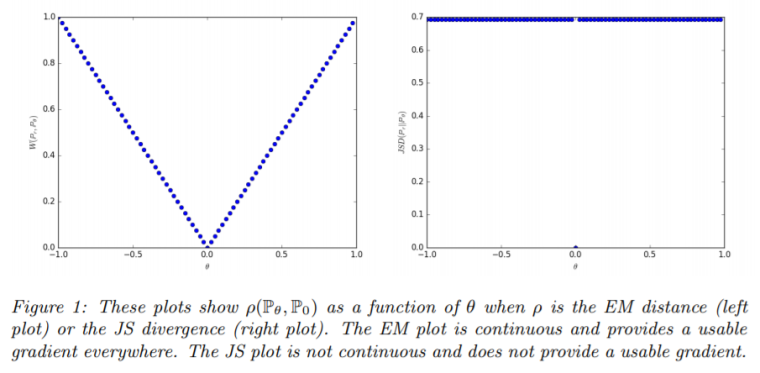
在上图中,Wasserstein(左图)自始自终都提供了很好的微分性质,我们的 SGD 可以得到方向正确、大小合理的梯度作为输入;但 JS(右图)梯度甚至在消失之前就已经是 0 了,SGD 根本就走不动。可见,当需要将两个概率分布的相似度作为梯度来训练神经网络时,Wasserstein 距离显然是非常合适的。
但这也存在一个问题。请看下面 Wassetstein 距离的定义
\[W(\mathbb{P}_r, \mathbb{P}_g) = \inf_{\gamma \in \prod(\mathbb{P}_r, \mathbb{P}_g)} \mathbb{E}_{(x, y) \sim \gamma} \big[ \Vert x - y \Vert \big]\]下确界?计算机可算不了一个解空间的下确界,但是经过 WGAN 作者一番操作之后(KR 对偶性、Lipschitz 连续性),终于导出了一个可用的梯度👇(具体证明我还没看懂也看不懂😂)
\[\nabla_{\theta} W(\mathbb{P}_r, \mathbb{P}_\theta) = - \mathbb{E}_{z \sim p(z)} \big[ \nabla_{\theta} f(g_\theta(z)) \big]\]把这个梯度 plug 到 GAN 里面去,Wasserstein distance + GAN = Wasserstein GAN !
\[\begin{align} &\textbf{while} \ \theta \ \text{has not converged} \ \textbf{do} \\ &\hspace{2em} \textbf{for} \ t = 0, \dots, n_{\text{critic}} \ \textbf{do} \\ &\hspace{4em} \text{Sample} \ \{ x^{(i)} \}_{i = 1}^{m} \sim \mathbb{P}_r \ \text{a batch from the real data.} \\ &\hspace{4em} \text{Sample} \ \{ z^{(i)} \}_{i = 1}^{m} \sim p(z) \ \text{a batch of prior samples.} \\ &\hspace{4em} g_w \leftarrow \nabla_w \big[ \frac{1}{m} \sum_{i = 1}^{m} f_w(g_\theta(z^{i})) \big] \\ &\hspace{4em} w \leftarrow w + \alpha \cdot \mathrm{RMSProp}(w, g_w) \\ &\hspace{4em} w \leftarrow \mathrm{clip}(w, -c, c) \\ &\hspace{2em} \textbf{end for} \\ &\hspace{2em} \text{Sample} \ \{ z^{(i)} \}_{i = 1}^{m} \sim p(z) \ \text{a batch of prior samples.} \\ &\hspace{2em} g_\theta \leftarrow - \nabla_\theta \frac{1}{m} \sum_{i = 1}^{m} f_w(g_\theta(z^{(i)})) \\ &\hspace{2em} \theta \leftarrow \theta - \alpha \cdot \mathrm{RMSProp}(\theta, g_\theta) \\ &\textbf{end while} \end{align}\]