TOC

• 什么是 / 为什么是 “强化学习”？
• 线性二次调节器（LQR）
• 了解世界
  • ==DAgger==
• 独当一面
  • Markov 决策过程
  • ==策略梯度==

---

什么是 / 为什么是 “强化学习”？

What? And why?

---

\[\text{maximize } r\]

问题解释：假设你在玩 地球OL，如何成为人生赢家？

• 我们受现实制约：\(s \in \mathbb{S}\)
  • 而且时常我们无法得知事情的真相：\(o \subset s \text{ or } o \sim s\)
• 我们能做的事情有限：\(a \in \mathbb{A}\)
• 我们心里对自己有数：\(s, a, s' \Rightarrow_{\tau, b} r\)
• 我们能与环境互动！ \(s, a \Rightarrow_{\pi, p} s'\)

---

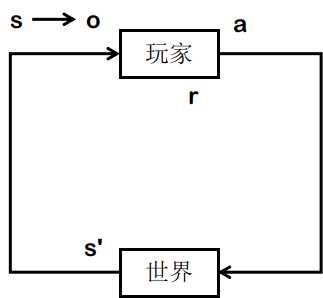
• 类似于人类的学习机制
  • “如果好吃你就多吃点”：\(\text{if } r^\star \uparrow, \text{ then } \uparrow p(s\vert_{r \approx r^\star})\)
• 一种可能的达成 AGI 的途径

---

线性二次调节器

Linear Quadratic Regulator

---

• 最优设计算法
  • 控制论
• 世界模型：\(\mathbf{x}_{t+1} = f(\mathbf{x}_t, \mathbf{u}_t) = \mathbf{F}_t \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix} + \mathbf{f}_t\)

  允许包含高阶项 \(\dot{x}, \ddot{x}, \cdots\)

• 评判标准：\(c(\mathbf{x}_t, \mathbf{u}_t) = \frac{1}{2} \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^T \mathbf{C}_t \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix} + \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^T \mathbf{c}_t\)
• 目标：\(\min_\tau \sum c\)
  • 注意对 \(\mathbf{x}\) 递归带入 \(f\)

---

\[\begin{align} &\text{/* 1. Backward recursion */} \\ &\text{for } t = T \text{ to } 1 \text{:} \\ &\hspace{1em} \mathbf{Q}_t = \mathbf{C}_t + \mathbf{F}_t^T \mathbf{V}_{t+1} \mathbf{F}_t \\ &\hspace{1em} \mathbf{q}_t = \mathbf{c}_t + \mathbf{F}_t^T \mathbf{V}_{t+1} \mathbf{f}_t + \mathbf{F}_t^T \mathbf{v}_{t+1} \\ &\hspace{1em} Q(\mathbf{x}_t, \mathbf{u}_t) = \mathrm{const} + \frac{1}{2} \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^T \mathbf{Q}_t \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix} + \begin{bmatrix} \mathbf{x}_t \\ \mathbf{u}_t \end{bmatrix}^T \mathbf{q}_t \hspace{2em} \text{(total cost from now until end if take } \mathbf{u}_t \text{ from state } \mathbf{x}_t \text{)} \\ &\hspace{1em} \mathbf{u}_t \leftarrow \arg \min_{\mathbf{u}_t} Q(\mathbf{x}_t, \mathbf{u}_t) = \mathbf{K}_t \mathbf{x}_t + \mathbf{k}_t \\ &\hspace{1em} \mathbf{K}_t = -\mathbf{Q}_{\mathbf{u}_t, \mathbf{u}_t}^{-1} \mathbf{Q}_{\mathbf{u}_t, \mathbf{x}_t} \\ &\hspace{1em} \mathbf{k}_t = -\mathbf{Q}_{\mathbf{u}_t, \mathbf{u}_t}^{-1} \mathbf{q}_{\mathbf{u}_t} \\ &\hspace{1em} \mathbf{V}_t = \mathbf{Q}_{\mathbf{x}_t, \mathbf{x}_t} + \mathbf{Q}_{\mathbf{x}_t, \mathbf{u}_t} \mathbf{K}_t + \mathbf{K}_t^T \mathbf{Q}_{\mathbf{u}_t, \mathbf{x}_t} + \mathbf{K}_t^T \mathbf{Q}_{\mathbf{u}_t, \mathbf{u}_t} \mathbf{K}_t \\ &\hspace{1em} \mathbf{v}_t = \mathbf{q}_{\mathbf{x}_t} + \mathbf{Q}_{\mathbf{x}_t, \mathbf{u}_t} \mathbf{k}_t + \mathbf{K}_t^T \mathbf{Q}_{\mathbf{u}_t} + \mathbf{K}_t^T \mathbf{Q}_{\mathbf{u}_t, \mathbf{u}_t} \mathbf{k}_t \\ &\hspace{1em} V(\mathbf{x}_t) = \mathrm{const} + \frac{1}{2} \mathbf{x}_t^T \mathbf{V}_t \mathbf{x}_t + \mathbf{x}_t^T \mathbf{v}_t \hspace{2em} \text{(total cost from now until end from state } \mathbf{x}_t \text{)} \\ &\\ &\because \, \mathbf{x}_1 \text{ is given} \\ &\\ &\text{/* 2. Forward recursion */} \\ &\text{for } t = 1 \text{ to } T \text{:} \\ &\hspace{1em} \mathbf{u}_t = \mathbf{K}_t \mathbf{x}_t + \mathbf{k}_t \\ &\hspace{1em} \mathbf{x}_{t+1} = f(\mathbf{x}_t, \mathbf{u}_t) \end{align}\]

• iterative LQR：如果不能线性，就用泰勒展开
  • 是的，对轨迹上每个点展开

---

了解世界

Learn about the world

---

Version 1.0

1. 采集数据 \(\mathcal{D} = \{ (\mathbf{x}, \mathbf{u}, \mathbf{x}')_i \}\)
2. 从数据 \(\mathcal{D}\) 学习世界模型 \(f \leftarrow \min_f \sum_i \lVert f(\mathbf{x}_i, \mathbf{u}_i) - \mathbf{x}' \rVert^2\)

---

Version 1.0 出了什么问题？

想想巴甫洛夫的狗…

• \[\mathcal{D}_0 \, := \{ (\text{ring bell and food}, \cdots\})\]
• \[f_{\mathcal{D}_0} = (\text{bell} = \text{food})\]
• \[\pi_{\mathcal{D}_0} = (\text{if bell, then go to front door for food})\]

被训练集教坏的模型！

• \(\mathcal{D}\) 并不能代表 \(\mathbb{S}\)，因为 \(\mathbf{x}_{\mathcal{D}} \subset \mathbb{S}\)

---

Version 2.0 - DAgger

Data Aggregation

1. 初始化 \(\pi_0\)
2. 跑 \(\pi_0\) 采集数据 \(\mathcal{D}\)
3. 从 \(\mathcal{D}\) 学习 \(f\)
4. 更新 \(\pi\) 为 \(\pi_i\)
5. 跑 \(\pi_i\) 采集数据 \(\mathcal{D}_i\)
6. [DAgger] \(\mathcal{D} := \mathcal{D} \cup \mathcal{D}_i\)
7. 回到步骤 3，直至收敛

---

独当一面

Be the master of yourself

---

Markov Decision Process

\[\pi(s) := \arg \max_a \{ \sum_{s'} P_a(s, s') ( R_a(s, s') + \gamma V(s') ) \}\] \[V(s) := \sum_{s'} P_{\pi(s)} ( R_{\pi(s)}(s, s') + \gamma V(s') )\]

from WikiPedia

---

评价方法

• 策略表现：\(\eta(\pi) = \mathbb{E} [ \sum_t \gamma^t r_t ]\)
• 状态评分：\(V_\pi(s) = \mathbb{E} [ \sum_t \gamma^t r_t \vert s_0 = s ]\)
• 状态-动作评分：\(Q_\pi(s, a) = \mathbb{E} [ \sum_t \gamma^t r_t \vert s_0 = s, a_0 = a ]\)

\(\gamma\) 为衰减因子

---

策略梯度

Prolicy Gradient

---

\[\text{maximize } \mathbb{E} [ R \vert \pi_\theta ]\]

基本思路

• 让好的轨迹更容易发生
• 让好的动作更容易发生
• 改善不好的动作

---

\[\begin{align} \nabla_\theta \mathbb{E}_x [ f(x) ] &= \nabla_\theta \int dx \, p(x \vert \theta) f(x) \\ &= \int dx \, \nabla_\theta p(x \vert \theta) f(x) \\ &= \int dx \, p(x \vert \theta) \frac{\nabla_\theta p(x \vert \theta)}{p(x \vert \theta)} f(x) \\ &= \int dx \, p(x \vert \theta) \nabla_\theta \log{p(x \vert \theta)} f(x) \\ &= \mathbb{E}_x [ f(x) \nabla_\theta \log{p(x \vert \theta)} ] \,. \end{align}\]

将 \(f(x)\) 替换为我们需要的任务目标

\[\hat{g} := \nabla_\theta \mathbb{E}_\tau [ R(\tau) ] = \mathbb{E}_\tau [ \nabla_\theta \log{p(\tau \vert \theta)} R(\tau) ]\]

• \[f \rightarrow R\]
• \[x \rightarrow \tau := (s_0, a_0, r_0, s_1, a_1, r_1, \cdots, s_{T-1}, a_{T-1}, r_{T-1}, s_T)\]

---

\[\hat{g} := \nabla_\theta \mathbb{E}_\tau [ R(\tau) ] = \mathbb{E}_\tau [ \nabla_\theta \log{p(\tau \vert \theta)} R(\tau) ]\]

现在研究 \(p(\tau \vert \theta)\)

• 在当前策略 \(\pi_\theta\) 下，当前关注的轨迹 \(\tau\) 发生的概率

\[\begin{align} p(\tau \vert \theta) &= \mu(s_0) \prod_{t=0}^{T-1} [ \pi(a_t \vert s_t, \theta) P(s_{t+1, r_t \vert s_t, a_t}) ] \\ \log{p(\tau \vert \theta)} &= \log{\mu(s_0)} + \sum_{t=0}^{T-1} [ \log{\pi(a_t \vert s_t, \theta)} + \log{P(s_{t+1}, r_t \vert s_t, a_t)} ] \\ \nabla_\theta \log{p(\tau \vert \theta)} &= \nabla_\theta \sum_{t=0}^{T-1} \log{\pi(a_t \vert s_t, \theta)} \\ \nabla_\theta \mathbb{E}_\tau[R] &= \mathbb{E}_\tau \bigg[ R \, \nabla_\theta \sum_{t=0}^{T-1} \log{\pi(a_t \vert s_t, \theta)} \bigg] \end{align}\]

---

\[\hat{g} := \nabla_\theta \mathbb{E}_\tau [ R(\tau) ] = \mathbb{E}_\tau [ R(\tau) \sum_t \nabla_\theta \log{\pi_\theta(a_t \vert s_t)} ]\]

现在需要定义 \(R(\tau)\) 了

• Q函数 / 状态-动作评分

  \[Q_{\pi, \gamma}(s, a) = \mathbb{E}_\pi [ r_0 + \gamma r_1 + \gamma^2 r_2 + \cdots \vert s_0 = s, a_0 = a ]\]

• 状态评分

  \[V_{\pi, \gamma}(s) = \mathbb{E}_{a \sim \pi} [ Q_{\pi, \gamma}(s, a) ]\]

• 进步评分

  • 在状态 \(s\) 时采取动作 \(a=\pi(s)\) 所能产生的评分提升

    \[A_{\pi, \gamma}(s, a) = Q_{\pi, \gamma}(s, a) - V_{\pi, \gamma}(s)\]

---

取其中一种形式

• Q函数
• reward-to-go
• 平均基准评分

得到

\[\hat{g} = \nabla_\theta \mathbb{E}_\tau[R] \approx \mathbb{E}_\tau \bigg[ \sum_{t=0}^{T-1} \nabla_\theta \log{\pi_\theta(a_t \vert s_t)} \bigg( \sum_{t' = t}^{T-1} \gamma^{t' - t} r_{t'} - b(s_t) \bigg) \bigg]\]

其中

• \[b(s_t) \approx \mathbb{E} [ r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \cdots + \gamma^{T-1-t} r_{T-1} ]\]

---

构建算法流程

1. 初始化策略网络参数 \(\theta\)，评价基准 \(b\)
2. （训练循环）
   1. 在环境 \(p\) 中跑当前策略 \(\pi\) 得到轨迹数据 \(\tau\)
      • 离散：\(a_t \sim \mathrm{M}\big( \pi_\theta(s_t), \mathbf{p}_a \big)\)
      • 连续：\(a_t \sim \mathrm{N}\big( \pi_\theta(s_t), \sigma \big)\)
   2. 对轨迹 \(\tau\) 中每一步 \(t\) 计算
      • 环境评分 \(R_t = \sum_{t'=t}^{T-1} \gamma^{t'-t} r_{t'}\)
      • 策略进步评价 \(\hat{A}_t = R_t - b(s_t)\)
   3. 更新评价基准 \(b \leftarrow \arg \min_b \sum_{t \in \tau} \lVert R_t - b(s_t) \rVert^2\)
      • 即将进步评价（的期望）归零
   4. 使用计算的策略梯度 \(\hat{g}\) 更新策略网络参数 \(\theta\)
      • 离散（交叉熵）：\(\mathrm{loss}_t := \mathrm{xent}\big( a_t , \pi_{\theta}(s_t) \big) \cdot \hat{A}_t\)
      • 连续（KL 散度）：\(\mathrm{loss}_t := - \log{\pi_\theta(a_t \vert s_t)} \cdot \hat{A}_t\)